[자료 구조 기초] Tree

Tree

---

Tree : 그래프의 구조 중 하나로 단방향 계층적 구조이며, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태이다.

Tree 구조 및 특징

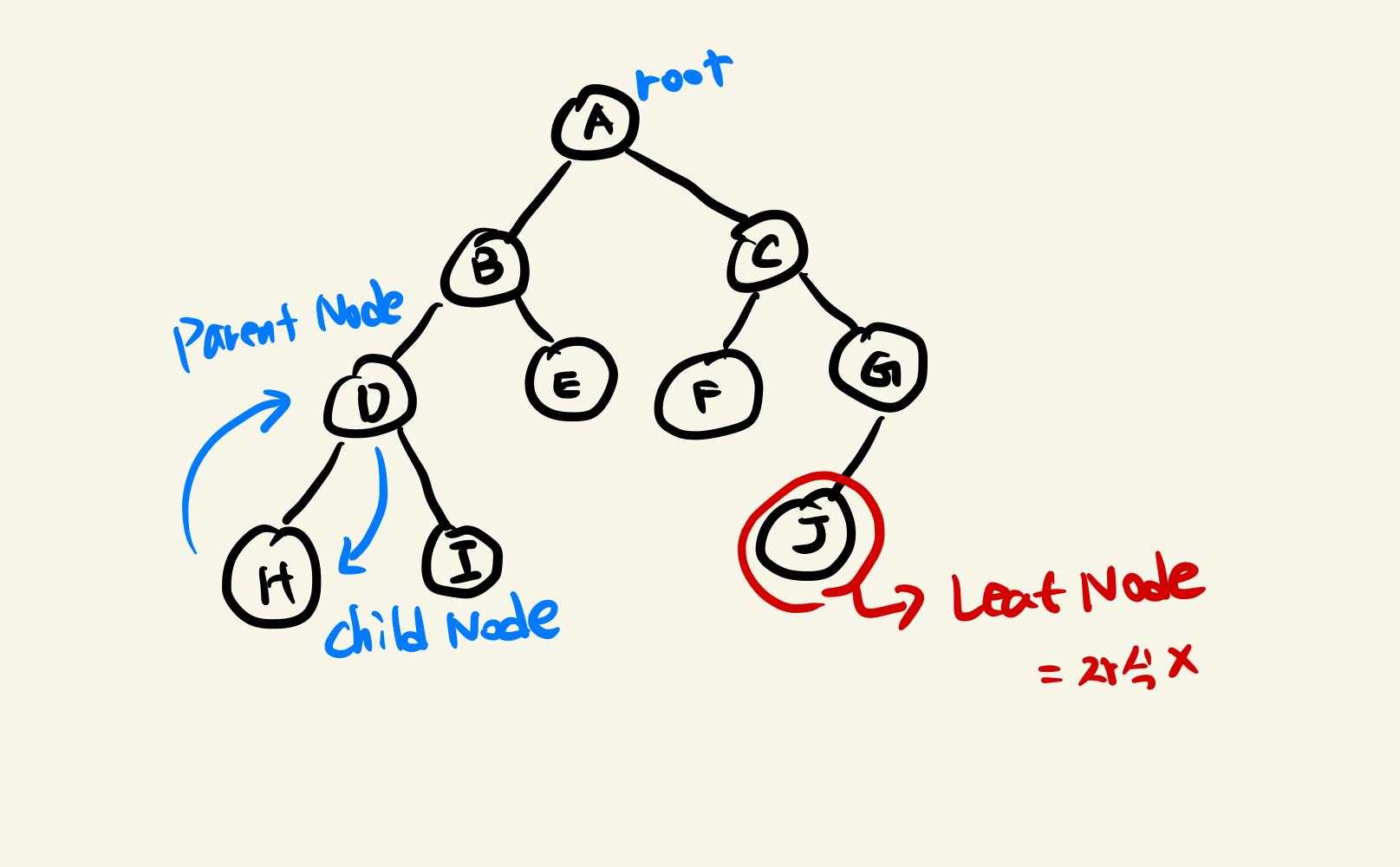
• Node : 트리 구조를 이루는 모든 개별 데이터
• Root : 트리 구조의 시작점이 되는 노드
• Parent Node : 두 노드가 상하관계로 연결되어 있을 때 상대적을으로 루트에서 가까운 노드
• Child Node : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
• Leaf Node : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드

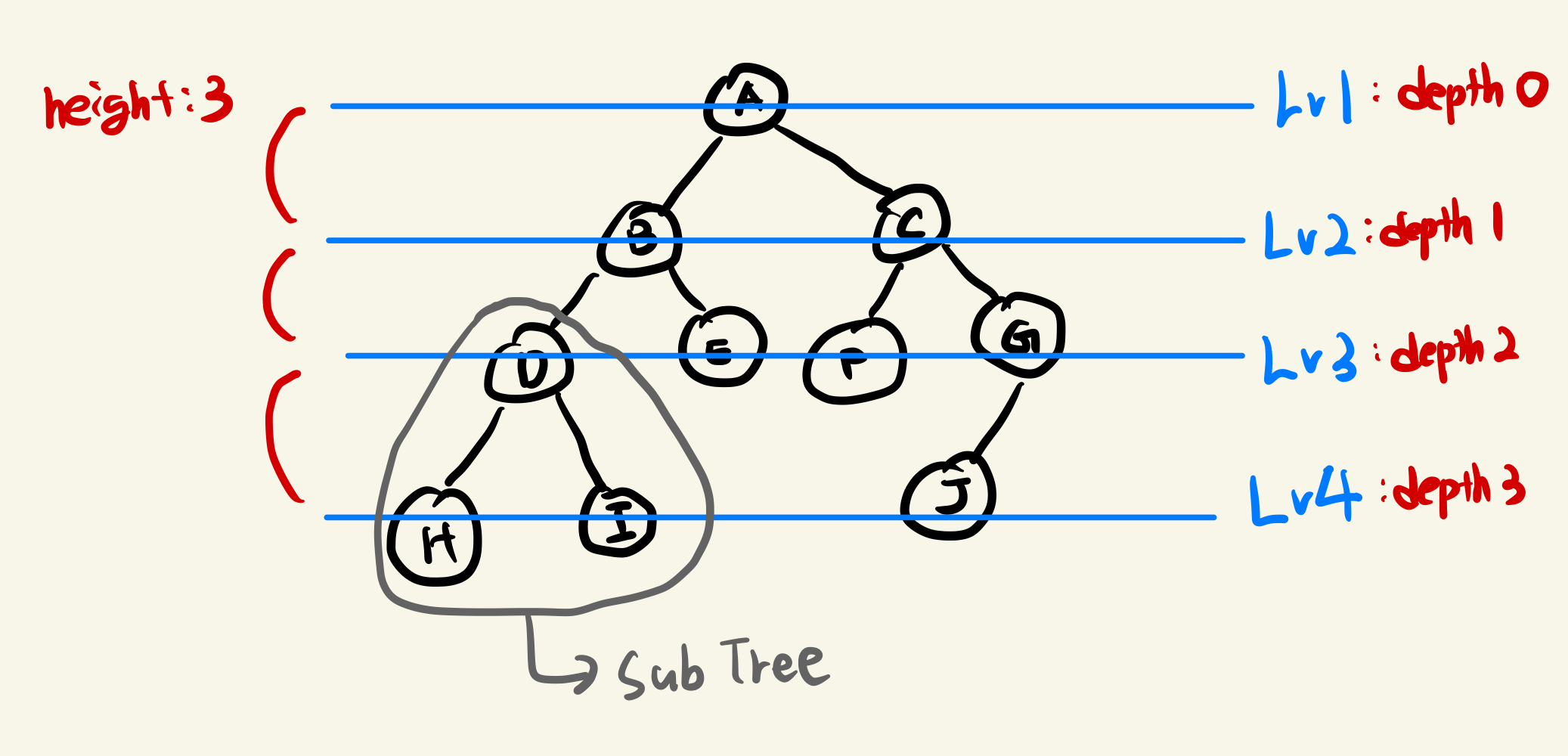
• Depth : 루트로부터 하위 계층의 특정 노드까지의 깊이
• Level : 같은 깊이를 가지고 있는 노드을 묶어서 레벨이라고 표현, 같은 레벨에 있는 노드를 형제 노드(Sibling Node)라고 한다.
• Height : 리프 노드를 기준으로 루트까지의 높이
• Sub Tree : 트리 구조를 갖춘 작은 트리

예제

---

class Tree {
    constructor(value) {
          // constructor로 만든 객체는 트리의 Node가 됩니다.
      this.value = value;
      this.children = [];
    }
  
      // 트리의 삽입 메서드를 만듭니다.
    insertNode(value) {
      const childNode = new Tree(value);
      this.children.push(childNode);
    }
  
      // 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
    contains(value) {
      if (this.value === value ) {
        return true;
      }
      
      for(let i=0;i<this.children.length;i++) {
        if(this.children[i].contains(value)) {
            return true
        }
      }
      
          // 전부 탐색했음에도 불구하고 찾지 못했다면 false를 반환합니다.
      return false;
    }
  }

BST : Binary Search Tree(이진 탐색 트리)

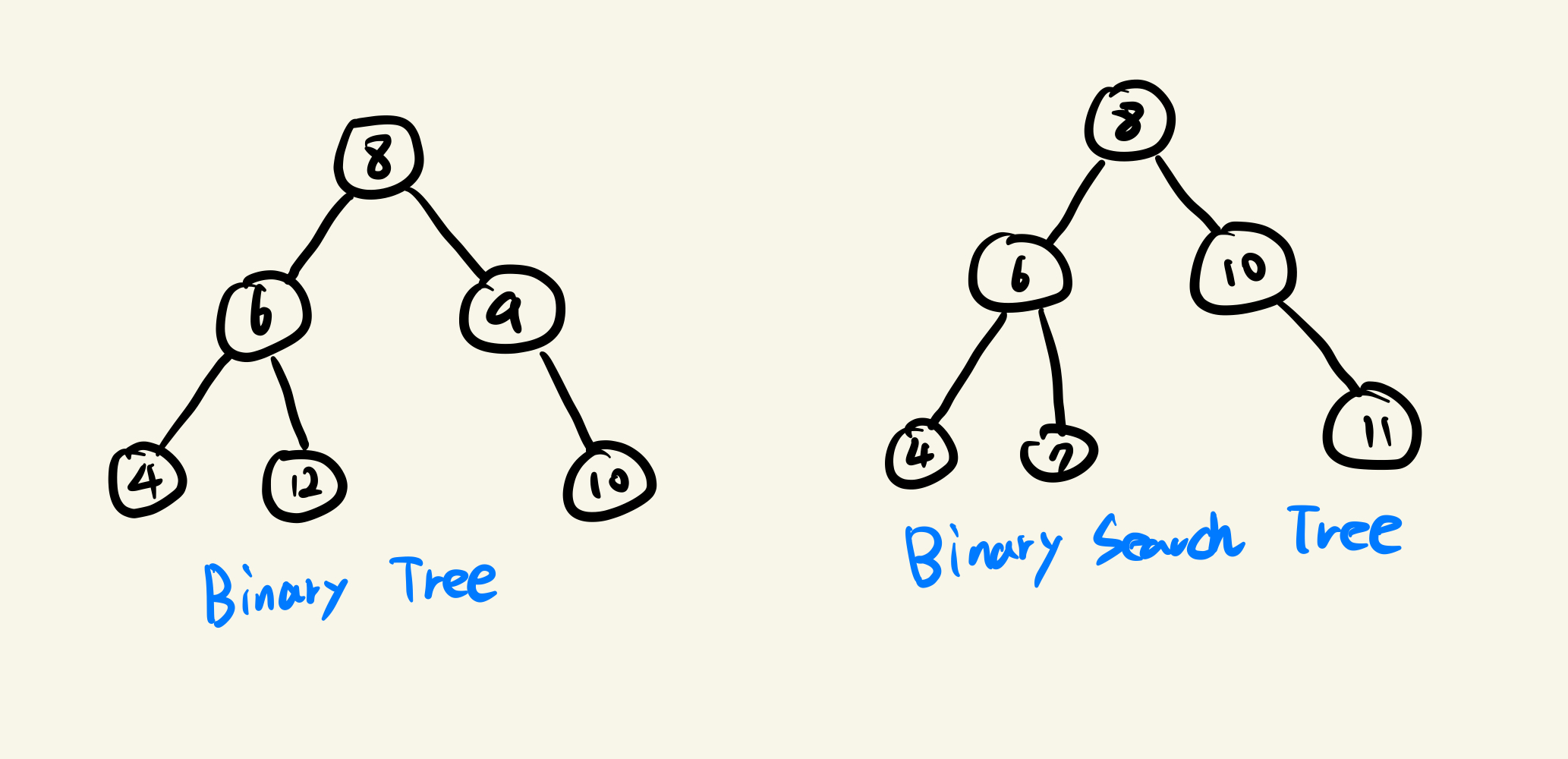
이진 트리 : 자식 노드가 최대 두개인 노드들로 구성된 트리

이진 탐색 트리 : 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 트리

Tree Traversal(트리 순회) -> Graph의 DFS에 포함된다.

---

Preorder(전위 순회)

---

1. Root
2. Left
3. Right

순으로 순회

Inorder(중위 순회)

---

1. Left
2. Root
3. Right

순으로 순회

Postorder(후위 순회)

---

1. Left
2. Right
3. Root

순으로 순회

예제

---

class BinarySearchTree {
    constructor(value) {
          // constructor로 만든 객체는 이진 탐색 트리의 Node가 됩니다.
      this.value = value;
      this.left = null;
      this.right = null;
    }
  
      // 이진 탐색 트리의 삽입하는 메서드를 만듭니다.
    insert(value) {
          // 입력값을 기준으로, 현재 노드의 값보다 크거나 작은 것에 대한 조건문이 있어야 합니다.
          // 보다 작다면, Node의 왼쪽이 비어 있는지 확인 후 값을 넣습니다.
      if (value < this.value) {
        if (this.left === null) {
          this.left = new BinarySearchTree(value);
        } else {
          return this.left.insert(value);
        }
          // 보다 크다면, Node의 오른쪽이 비어 있는지 확인 후 값을 넣습니다.
      } else if (value > this.value) {
        if (this.right === null) {
          this.right = new BinarySearchTree(value);
        } else {
          return this.right.insert(value);
        }
          //그것도 아니라면, 입력값이 트리에 들어 있는 경우입니다.
      } else {
        // 아무것도 하지 않습니다.
        return
      }
    }
      // 이진 탐색 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
    contains(value) {
      if (this.value === value) {
        return true;
      }
          // 입력값을 기준으로 현재 노드의 값보다 작은지 판별하는 조건문이 있어야 합니다.
      if (value < this.value) {
        if(this.left && this.left.contains(value)) {
          return true;
        }
      }
          // 입력값을 기준으로 현재 노드의 값보다 큰지 판별하는 조건문이 있어야 합니다.
      if (value > this.value) {
              if(this.right && this.right.contains(value)) {
          return true;
        }
      }
          // 없다면 false를 반환합니다.
      return false
    }
  
      /*
      트리의 순회에 대해 구현을 합니다.
    지금 만드려고 하는 이 순회 메서드는 단지 순회만 하는 것이 아닌, 함수를 매개변수로 받아 콜백 함수에 값을 적용시킨 것을 순회해야 합니다.
    전위 순회를 통해 어떻게 탐색하는지 이해를 한다면 중위와 후위 순회는 쉽게 다가올 것입니다.
      */
  
      // 이진 탐색 트리를 전위 순회하는 메서드를 만듭니다.
    preorder(callback) {
          callback(this.value); //root
      if (this.left) {
        this.left.preorder(callback);
      };
      if (this.right) {
        this.right.preorder(callback);
      };
    }
  
      // 이진 탐색 트리를 중위 순회하는 메서드를 만듭니다.
    inorder(callback) {
      if (this.left) {
        this.left.inorder(callback);
      };
      callback(this.value) //root
      if (this.right) {
        this.right.inorder(callback);
      };
    }
  
      // 이진 탐색 트리를 후위 순회하는 메서드를 만듭니다.
    postorder(callback) {
      if (this.left) {
        this.left.postorder(callback);
      };
      if (this.right) {
        this.right.postorder(callback);
      };
      callback(this.value) //root
    }
  
  }
  
  const rootNode = new BinarySearchTree(10);
  rootNode.insert(7);
  rootNode.insert(8);
  rootNode.insert(12);
  rootNode.insert(11);
  console.log(rootNode.left.right.value); // 8
  console.log(rootNode.right.left.value); //11
  
  let arr = [];
  rootNode.preorder((value) => arr.push(value * 2));
  console.log(arr); // [20, 14, 16, 24, 22]

본 포스팅은 코드스테이츠 BEB 과정을 수강하며 작성한 글입니다.